Optische Qualität
Zur Bemessung der optischen Fehler, d.h. Oberflächengenauigkeit oder Bildfehler, Oberflächenglätte oder -rauhigkeit, Peak to Valley oder Root Mean Square, könnte man ein ganzes Buch schreiben. Auch darüber, wie eigentlich bescheidene Werte geschönt werden. Bereits die gängigen, handelsüblichen Bezeichnungen kommen eher einem Verwirrspiel gleich, das dem Nicht-Experten den Vergleich beworbener Zahlen schon fast unmöglich macht. Ohne genaue Definition ist jeder beworbene Wert nutzlos.
Maßeinheit Wellenlänge
Als Maßeinheit dient die Länge einer Lichtwelle. Das Wahrnehmungsmaximum des Auges liegt am Tag bei einer Wellenlänge von ca. 560 nm (Nanometer) bzw. 5600 Angström (Quecksilbergrün), was 560 millionstel Millimeter entspricht. Eine volle Wellenlänge mag in mm ausgedrückt sehr klein aussehen. Bei einem Spiegel wäre das bereits ein derber Oberflächenfehler, den jeder mit seinen Augen sehen kann, bei entsprechender Vergleichsmöglichkeit und ohne jegliches Hilfsmittel. Normalerweise verwendet man Bruchteile (l/4) der Wellenlänge, die auch als Dezimal-Anteil (0,25) dargestellt werden können. Besonders wissenschaftliche Anbieter verwenden den griechischen Buchstaben Lambda (l) als Bezeichnung für das Wort Wellenlänge.
Beispiel: 1/4 Lambda = 1/4 l = l/4 = 1/4 Wellenlänge = 0,25 Wellenlängen = 0,25 l = 0,25 Lambda
Je nach Farbe sind Lichtwellen unterschiedlich lang. Lambda, l oder die Wellenlänge hat keine bestimmte Länge, es kann also eine beliebig lange Lichtwelle als Messlatte hergenommen werden, mit entsprechend schöner dargestellter Oberflächengenauigkeit. Beim Interferometer wird meist mit Helium-Neon Laser gearbeitet, d.h. die Messlatte ist 6328 Angström bzw. 632 nm lang. Das Ergebnis wird also um 12,5% besser dargestellt als mit 560 nm. Dem Anbieter stellt sich hier die Frage, weshalb ein wissenschaftlich korrekt erstelltes Testprotokoll um 12,5% gekürzt werden sollte, um mit der Darstellungsform von Daumen mal Auge Messungen gleichzuziehen.
Oberflächengenauigkeit/Bildgenauigkeit
Es gibt zwei grundverschiedene Möglichkeiten, wo die optische Qualität gemessen bzw. dargestellt wird.
Bildgenauigkeit (wavefront)
Die Bildgenauigkeit, meistens als "wavefront"-Fehler bezeichnet, bezieht sich auf das Bildergebnis, das entweder aus einem Gesamtsystem herauskommt, oder von einem einzelnen optischen Element geliefert wird, was auch schon wieder einen erheblichen Unterschied machen kann. Es wird hier die maximale Phasenverschiebung der Lichtwellen im Brennpunkt dargestellt. Wenn in der Literatur usw. Mindestanforderungen an die Abbildungsleistung gestellt werden, ist fast immer wavefront im Brennpunkt eines Gesamtsystems gemeint.
Oberflächengenauigkeit
Die Oberflächengenauigkeit bezieht sich auf die Oberflächenqualität einer einzelnen optischen Fläche, bzw. deren Abweichung von der theoretischen Idealform. Wenn Spiegelteleskope angeboten werden, wird fast immer nur die Oberflächengenauigkeit des Hauptspiegels beworben. Bei einem Newton-Hauptspiegel mit z.B. 1/4 Wellenlänge Oberflächengenauigkeit ergibt sich, da das Licht den Fehler zweimal zurücklegt, zum Spiegel hin und nochmals zurück, ein Bildfehler von 1/2 l. Bei Systemen mit mehreren Komponenten addieren sich die Fehler.
Darstellungs- u. Bewertungsmethoden
Bild- und Oberflächengenauigkeit lassen sich nun mit unterschiedlichen Bewertungsmethoden zu höchst unterschiedlichen Ergebnissen umdeuten. Alles läßt sich natürlich beliebig kombinieren. Die Bewertungsmethoden PV (Peak to valley) RMS (Root Mean Square) führen zu sehr unterschiedlichen Ergebnissen, haben aber beide ihre Berechtigung + / - Mit plus/minus liest sich der beworbene Wert doppelt so gut, ein anderer Grund hierfür ist mir nicht bekannt. ca. Statt der unteren Produktionstoleranz oder individuellen Messergebnissen kann auch die durchschnittliche Produktionsgenauigkeit beworben werden. Für die Abbildungsleistung ist die Mindestgenauigkeit der jeweiligen Optik maßgeblich.
PV (Peak to Valley)
PV drückt die Gesamttoleranz von der Spitze bis zum Tal, von der höchsten bis zur tiefsten festgestellten Abweichung von der theoretischen Idealform aus. Diese "konservative" Darstellung der Oberflächen- oder Bildgenauigkeit hat ihren Ursprung in althergebrachten Testmethoden, z.B. mit dem Foucault-Test aus dem Jahre 1857. Wenn ein Foucault Test über 7 Testzonen gemacht wird und der Tester daraus einen PV-Wert ermittelt, hat dies seine Berechtigung.
Bei modernen Testmethoden, wie z.B. einem Interferogramm mit Computerauswertung, hat der PV-Wert kaum Aussagekraft und Berechtigung. PV drückt letztendlich nur den Abstand zwischen zwei Punkten aus, dem höchsten und dem tiefsten Meßwert. Wenn über 50.000 Testpunkte absolut präzise vermessen und vom Computer verrechnet werden, ist eine auf 2 von 50.000 Daten gestützte Aussage unsinnig und irreführend.
PV - Oberflächenrauhigkeit
Selbst bei tatsächlich gleicher PV-Oberflächengenauigkeit können zwei Spiegel höchst unterschiedliche Bilder liefern. Im durch die Oberflächengenauigkeit bezeichneten Bereich zwischen oberer und unterer Abweichung von der Idealform des Spiegels kann eine "rauhe" Oberfläche, übertrieben ausgedrückt, wie Schleifpapier aussehen, d.h. eine sehr große Lichtstreuung und damit einen großen Verlust an Kontrastschärfe verursachen; speziell maschinenpolierte Spiegel tendieren in diese Richtung. Eine "glatte" Oberfläche schwankt innerhalb der gleichen Grenzen wesentlich sanfter, und liefert eine wesentlich bessere Kontrastschärfe. Der PV-Wert berücksichtigt weder Häufigkeit und Verteilung der Fehler, noch läßt er Rückschlüsse auf die Oberflächenrauhigkeit und damit die Kontrastleistung zu.
PV - beugungsbegrenzt nach Rayleigh
Eine brauchbare Optik muß nach Rayleigh Bilder mit min. 1/4 PV wavefront liefern. Diese Bildgenauigkeit setzt die doppelte Oberflächengenauigkeit eines Spiegels voraus. Eine Bildgenauigkeit von weniger als 1/4 PV wavefront begrenzt öffnungsabhängig die mögliche bzw. sinnvolle Vergrößerung. Zur groben Orientierung sollte bei einer Bildgenauigkeit von 1/1 bzw. 1/2,5 PV wavefront die Austrittspupille nicht kleiner sein als als ca. 3 bzw. 1,25 mm. Das hier gesagte und das von Lord Rayleigh zu Beginn dieses Jahrhunderts formulierte Kriterium gilt für PV-Werte, die mit der "manuellen" Testmethode ermittelt werden, wie sie von Foucault bereits seit dem Jahre 1857 praktiziert wurde.
RMS
Zunächst muß sich die Industrie den Vorwurf gefallen lassen, daß RMS auch der geschönten Zahlendarstellung dient. RMS, Root Mean Square, ist eine gemittelte Durchschnittsabweichung, der RMS-Wert ist mindestens 3,3 mal schöner als der PV-Wert. Besonders unfair ist, wenn RMS-Werte beworben werden, ohne ausdrücklich als solche gekennzeichnet zu sein.
Wenn man RMS-Werte als solche erkennt und damit umgehen kann, lassen sie genaue Rückschlüsse auf die Abbildungsleistung eines Teleskopes zu. Bei modernen Testprotokollen, d.h. Interferogramm mit Computerauswertung, ist der RMS-Wert die einzige sinnvolle Auswertung. Wie RMS, PV und Kontrastleistung zusammenhängen, zeigt folgende Abbildung:
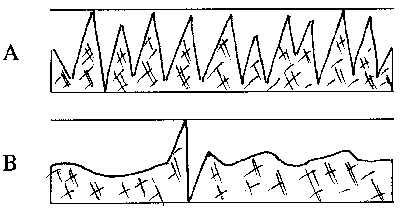
Spiegel A und Spiegel B weisen die gleiche PV-Oberflächengenauigkeit von 1/4 PV auf. Spiegel A ist "rauh", d.h. die Spiegeloberfläche schwankt ständig zwischen Maximum und Minimum. Wahrscheinlich enthält dieser Spiegel eine Stelle mit größerem Fehler, die in dieser Messung nicht gefunden wurde. Die RMS-Oberflächengenauigkeit beträgt nur 1/16 RMS, die von diesem Spiegel gelieferte Kontrastschärfe ist unbrauchbar.
Spiegel B hat die gleiche PV-Oberflächengenauigkeit von 1/4 PV. Dieser Oberflächenfehler ist jedoch auf 1/1000 der Gesamtfläche begrenzt, und bei einem scharf gestellten Bild defakto unsichtbar. Mit etwas Glück oder bei entsprechender Anzahl von Messungen wäre diese Stelle auch durch den Messraster gefallen, d.h. dieser Spiegel könnte genausogut eine Genauigkeit von 1/8 PV im Protokoll haben. Bei der RMS-Auswertung fließt die Glätte des Spiegels erheblich ins Messergebnis ein, der Spiegel ist besser 1/30 RMS. Mit kleiner Obstruktion kommt die Kontrastschärfe in brauchbare Bereiche.
Diese beiden Extrembeispiele sind von der Praxis gar nicht so weit entfernt. Jeder erfahrene Astronom kennt die Regel, daß die Kontrastleistung eines Spiegels nicht direkt aus dem PV Oberflächenwert abzuleiten ist, sondern eben auch entscheidend die Glätte hinzu kommt. Das extremste mir bis jetzt bekannte Testprotokoll weist für einen 10" f/4,8 eine PV wavefront Bildgenauigkeit von "nur" 1/3,6 aus, also nicht mal 1/4 PV. Wenn man sich nicht auf nur 2 Meßwerte beschränkt sondern die übrigen 50.000 digital ermittelten Meßwerte zu Rate zieht, kommt ein RMS-Wert von 1/28 wavefront heraus. Daneben weist das Protokoll einen Strehl-Wert von 0,95 aus, d.h. die Optik ist gerade mal 5% schlechter als ein theoretisches Ideal. Ohne Zweifel würde ein Interferogramm über 500 Testpunkte einen deutlich besseren PV-Wert ausweisen, und jeder manuelle Test würde die Oberflächengenauigkeit im Bereich von 1/20 PV ansiedeln.
Strehl-Wert bzw. Definitionshelligkeit
Die meisten Computerauswertungen weisen noch den Strehl-Wert aus, der direkt aus dem RMS-Wert errechnet wird. Im deutschsprachigen Raum hat sich auch der Begriff Definitionshelligkeit hierfür eingebürgert. Der Strehl gibt direkten Aufschluß über die Abbildungsleistung der Optik. Er weist den Anteil des Lichtes aus, der nicht mangels optischer Perfektion zusätzlich in die Beugungsringe verloren geht, sondern für die Beobachtung im Beugungsscheibchen zur Verfügung steht. Jede Optik hat natürlich weitere, systembedingte Verluste, die lassen sich aber nicht vermeiden, und werden beim Strehl nicht berücksichtigt. Eine völlig perfekte Optik bringt 100% des Lichtes, das theoretisch im Beugungsscheibchen landen kann, auch dorthin; das würde in einem Strehl-Wert von 100% oder 1.00 ausgedrückt. Weniger als 0,50 ist im Massenmarkt eher die Regel, und ab 0,80 kann man seine Optik durchaus als gut einstufen.
Fangspiegelgröße / Obstruktion
Der Aspekt des relativ geringen Flächen- bzw. Lichtverlustes durch große Obstruktionsdurchmesser veranlaßt oft zur Überdimensionierung des Fangspiegels. Jedoch ist ausschließlich der Fangspiegel-Durchmesser im Vergleich zur Öffnung für den obstruktionsbedingten Kontrastschärfeverlust entscheidend. Während für Fotografie selbst 50% Obstruktion ohne Beeinträchtigung der fotografischen Bildschärfe möglich sind, ist für meinen Geschmack für visuelle Beobachtung eine sehr gute Kontrastschärfe nur mit max. 20% Obstruktion möglich. Der Fangspiegel sollte auf jeden Fall so klein wie irgend möglich sein. Folgende vereinfachte Formel enthält bereits etwas Aufschlag. Visuell ist für jedes Okular ein zu 100% ausgeleuchtetes Bildfeld von 10mm mehr als ausreichend. Entscheidend für die Fangspiegelgröße ist die Höhe des Okularauszuges, der bei niedriger Bauhöhe eine deutliche Verkleinerung des Fangspiegels zuläßt. Für Fotografie sind größere Fangspiegel nötig. Ausleuchtung in der Bildecke sollte mindestens 60-70% sein, engagierte Fotografen werden zu besserer Ausleuchtung neigen. Der Helligkeitsabfall außerhalb des Bildfeldes ist vom Öffnungsverhältniss und der Höhe des Okularauszuges abhängig. Bei niedrigeren Okularauszügen ist die Ausleuchtung insgesamt besser, aber der Helligkeitsabfall deutlich steiler. Ich würde deshalb bei der Bemessung der Fangspiegelgröße für KB-Fotografie von einem min. 20 bis 25 mm großem 100% Bildfeld bei hohem Okularauszug ausgehen. Bei einem Kompromiß, der neben der Fotografie auch visuelle Beobachtung zulassen soll, sollte die Obstruktion unter 20%, auf jeden Fall unter 25% bleiben.
Faustregeln zur Berechnung der visuellen Kontrastschärfe nach William P. Zmek
In einem sehr guten, 2-teiligen Artikel in Sky&Telescope (July 93, Seite 91 und Sept. 93, Seite 83) hat William P. Zmek die Anregung und Formeln für dieses Kapitel geliefert. Die komplizierte Berechnung der Kontrastschärfe kann nach Zmek durch folgende Prämissen ziemlich vereinfacht werden:
- Alle Aussagen gelten nur für den durch das Auge wahrnehmbaren Bereich, d.h. die nicht wahrnehmbaren Bereiche bleiben unberücksichtigt.
- Alle Aussagen beziehen sich nur auf Details mit 20% Kontrast, wie er bei Planeten und DeepSky Objekten häufig vorkommt.
- Als Ergebnis berechnet Zmek nicht diffuse Wahrnehmungsverluste sondern harte Öffnungsverluste bzw. effektive Durchmesser.
Der Ansatz ist für mich absolut praxisbezogen, und macht Dinge, die wir eigentlich immer schon wissen, direkt rechenbar. Das Teleskop kann nicht mehr Kontrast liefern, als im Objekt vorhanden ist. Lichtverschmutzung und Luftunruhe reduzieren den Kontrast. Für das Teleskop gilt ein öffnungsbedingtes Limit. Die Kontrastleistung des Teleskopes resultiert aus der Summe aller Defekte, wie z.B. lokales Seeing, Obstruktion, Spinnenarme, Streulicht, Verschmutzung der Optik, Oberflächenfehler der Optik, Verbiegung und Deformation durch falsche Fassungen sowie falsche Justierung. Der Kontrastverlust durch die Spinnenarme oder deutliche Verschmutzung der Optik ist minimal, jeweils rund max. 1% Öffnungsverlust. Streulicht durch mangelhafte Blenden (im flachen Winkel hoch reflektive, matt schwarz lackierte Tubuswände) und lokales Seeing (z.B. den Strahlengang durchquerende Körperwärme von wartenden Gästen) können ganz erhebliche Verluste verursachen.
Vereinfachte Berechnung der Fangspiegelgröße
DF = A : f/ + B | A = TAR + BÜT |
| mit DF Durchmesser Fangspiegel | |
Grobe Richtwerte für den Helligkeitsabfall bei 10" Öffnung und 100 mm BüT
| Relative Bildhelligkeit | 90% | 80% | 70% | 60% |
| f/5 | DB +8mm | DB +14mm | DB +20mm | DB +28mm |
| f/6 | DB +6mm | DB +12mm | DB +17mm | DB +22mm |
| DB+ = zusätzlicher Durchmesser zum 100% Bildfeld | ||||
Obstruktion
Der alte Streit zwischen Refraktor und Reflektor kann ganz einfach geklärt werden: Die Kontrastübertragung eines Teleskopes mit zentraler Obstruktion ist die gleiche wie bei einem nicht obstruierten Teleskop mit kleinerem Durchmesser. Die Berechnung stimmt ziemlich gut, bei sehr kleinen Obstruktionen ist der Kontrastverlust eher noch etwas geringer. Ein Newton mit 203 mm Öffnung und 33 mm Fangspiegel bringt also die Kontrastleistung eines nicht obstruierten Systems mit 170mm Öffnung. Ein 8"SC mit 43% Obstruktion kann maximal die Kontrastschärfe eines Refraktors mit 116 mm liefern. Voraussetzung für diese Aussage ist gleiche Qualität auf beiden Seiten.
DK = D - DF |
| mit DK = effektiver Kontrast-Durchmesser, mit gleicher visueller Wahrnehmung eines 20%igen Kontrastes |
Oberflächenfehler
Sphärische Abberation kann ganz erheblich die Kontrastleistung herabsetzen.
DK = D exp(-33E2) |
| mit DK = effektiver Kontrast-Durchmesser, |
Die Formel stimmt ziemlich genau bis wavefront 0,15 RMS, wobei hier bereits der zur Wahrnehmung eines 20%igen Kontrastes effektiv benutzte Durchmesser (DK) weniger als die halbe Öffnung ist. Mit der Formel von William P. Zmek habe ich folgende Tabelle berechnet. Wavefront und DK Effektiv gelten für alle Systeme gleichermaßen.
| Wavefront | N-Oberfläche | DK | |||
| RMS | RMS | PV | RMS | PV | Effektiv |
| l | l/ | l/ | l/ | l/ | % |
| 0,150 | 1/6,67 | 1/2 | 1/13 | 1/4 | 47% |
| 0,100 | 1/10 | 1/3 | 1/20 | 1/6 | 72% |
| 0,075 | 1/13,3 | 1/4 | 1/26 | 1/8 | 83% |
| 0,060 | 1/16,7 | 1/5 | 1/33 | 1/10 | 89% |
| 0,050 | 1/20 | 1/6 | 1/40 | 1/12 | 92% |
| 0,038 | 1/26,7 | 1/8 | 1/53 | 1/16 | 95% |
| 0,030 | 1/33.3 | 1/10 | 1/66 | 1/20 | 97% |
| 0,025 | 1/40 | 1/12 | 1/80 | 1/24 | 98% |
N-Oberfläche gilt nur für Newton oder andere Ein-Spiegel-Systeme (Da alle anderen gängigen Systeme normalerweise mit einem Zenithprisma bzw. -Spiegel benutzt werden, kann der Newton-Fangspiegel beim Vergleich weggelassen werden.)
Mit einer N-Oberflächengenauigkeit von 1/4 PV oder 1/13,3 RMS wird hinsichtlich der Kontrastschärfe weniger als der halbe Durchmesser benutzt. Wenn ein Hersteller ein 10" Newton mit einem 2,6" Fangspiegel bestückt und einen 1/4 PV Hauptspiegel einbaut, so kommt eben nur 3,5 Zoll effektiver Kontrast-Durchmesser heraus. Beim 8" SC mit 38% Obstruktion und Durchschnittsqualität sieht es nicht anders aus. Man braucht sich also nicht zu wundern, wenn ein guter 4-Zoll-Refraktor mehr zeigt. Ein gutes 8" Newton mit 1,5" Fangspiegel und 1/50 RMS Oberfläche hat dagegen selbst mit einem idealen 6-Zoll-Refraktor kein Problem.
Wunsch und Wirklichkeit
Nachdem nun feststeht, welche Werte ein gutes Teleskop bringen sollte, besteht "nur" noch ein praktisches Problem: Stehen fromme Wünsche auf geduldigem Papier, oder hat die gelieferte Optik die beworbene Qualität. Egal ob hochglanz-vierfarb oder kopiert, in fast allen Prospekten werden die weltbesten Teleskope beworben. Als "absolut beugungsbegrenzt" wird mittlerweile alles bezeichnet. In einem Prospekt werden Spiegel mit einer Oberflächengenauigkeit von "1/4 Wellenlänge" (PV oder RMS?) beworben, im Text erreichen sie das theoretische Auflösungsvermögen, was sich eigentlich gegenseitig ausschließt. Wenn dann noch absolute Inkompetenz den Fernrohrmarkt erobern will, entstehen Werbeaussagen wie z.B. "Aufgrund der besonderen Spiegelschleifmethode ... sind alle Spiegel absolut komafrei ...". Es wäre ja schön, aber leider sprechen beim paraboloiden Newton physikalische Gesetze dagegen. Dafür werden diese Wunderwerke mit geradezu phantastischer Genauigkeit beworben "Der sogenannte Wavefront-error liegt bei mindestens 1/20 peak to valley bei 560 nm" Liest sich gut und ist identisch mit 1/40 PV Oberfläche, d.h. eigentlich unvorstellbar gut, selbst mit dem Interferometer kaum zu messen, aber es geht noch weiter: "Dieser Wert wird jedoch erhöht, falls das Erscheinungsbild des Spiegels in Bezug auf Kontrast und Abbildungsverhalten es erfordert." Diese Aussage wäre nicht mal bei 25% der beworbenen Genauigkeit notwendig, wobei ich hiermit keine qualitative Untergrenze zum Ausdruck bringen will. Die ungeschickte Aneinanderreihung positivster Eigenschaften entlarvt sich von selbst, mit der Zeit werden diese Anbieter es lernen, realistischere Behauptungen aufzustellen. Etwas erfahrenere Billiganbieter garantieren "realistische" 1/8 bis 1/25 PV. Beim Nachmessen kommt dann nur 1/1 bis 1/4 PV heraus. Das "Rückgaberecht bei Nichteinhaltung der beworbenen Spezifikationen" haben Sie auch als gesetzlichen Anspruch, durchsetzen können Sie es mit einem beweiskräftigen Testprotokoll. Papier ist geduldig, und wer hat schon Vergleichsmöglichkeiten oder Prüfeinrichtungen. Deshalb nicht nur nach Prospektdaten kaufen. Bei Massenware unbedingt das Teleskop testen, das dann mitgenommen werden soll. Gehen Sie vor einer Kaufentscheidung auf ein Teleskoptreffen. Sie können dort viele verschiedene Teleskope testen, und sich selbst einen Eindruck verschaffen. Vertrauen Sie Ihren eigenen Augen. Sowie Sie einen Vergleich haben, können Sie selbst extrem feine Unterschiede feststellen. Sowie Sie sich die Bilder einer wirklich guten Optik eingeprägt haben, werden Sie eine schlechte Qualität sofort erkennen.




